蔡司雷竞技raybet1 测量实操讲解——最小二乘法拟合
坐标点拟合
坐标点数据需要经过计算机处理，拟合形成测量元素，比如直线、平面、圆、圆柱、圆锥等，再经过特定的数字计算方法得出其形状、位置公差以及其他几何量数据。
不太能理解？那我们举个例子。
假设我们要测量一个圆柱体零件
首先，为了简化问题难度我们将三维问题变为二维问题，只考虑XY坐标。在圆柱上任一截面，每间隔18°取一个测量点，一共取20个测量坐标点。并在X0Y坐标系里表示出来。
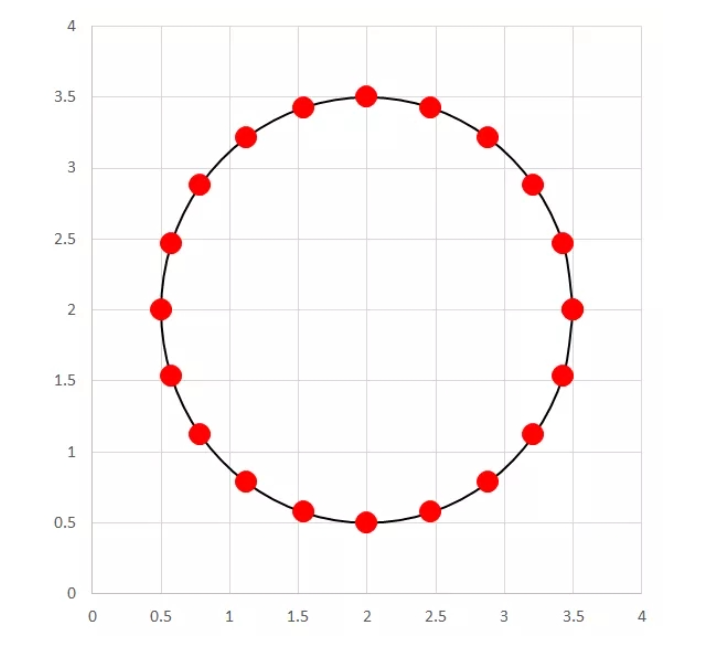
上面的图看起来是一个圆，但是问题没这么简单。这个世界上有一种东西叫误差，而误差是绝对存在的。简单来说，由于误差的存在，实际存在的东西和理论形状是有偏差的，比如说我们平时看到的平面，在微观尺度下是这样的：
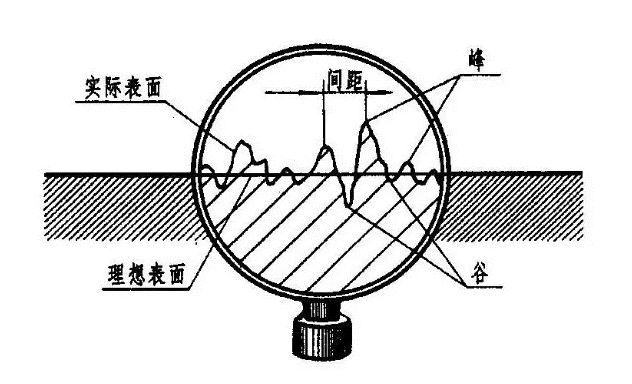
同样，由于机床本身的误差外加装夹误差、加工热误差、振动误差等原因。被加工圆实际上也不是理想圆，只是因为误差本身数值很小，肉眼难以分辨。为了让大家形象的观察到误差的存在，我们把刚才被测圆数据的误差放大几百倍，看似完美的圆就变成了下面的不规则多边形：
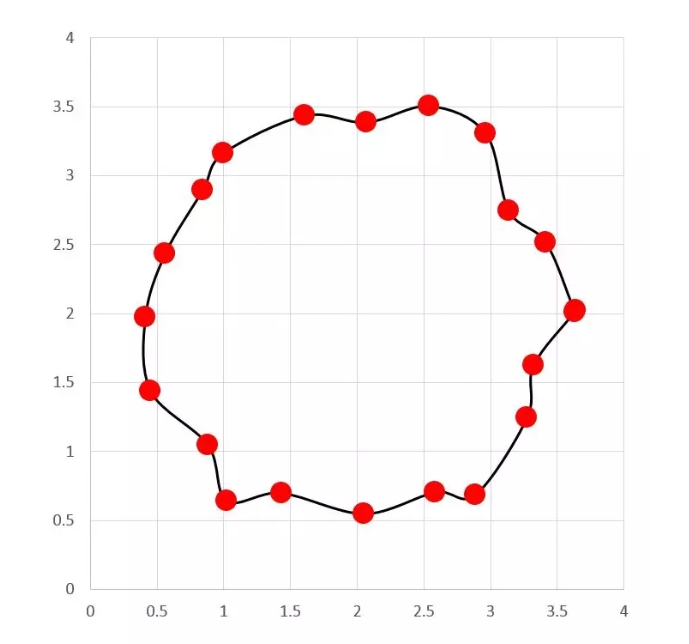
此时，我们不难看出，这些实测坐标点似乎不像一个圆。但是，它又的的确确是一个实际圆柱上的坐标值。那么问题来了：
它的直径是多少？
它的圆心又在哪里？
此刻，我们需要找一个理想的圆来表示出这个实际上并不理想的圆，这个过程就是前面提到的坐标点拟合过程：
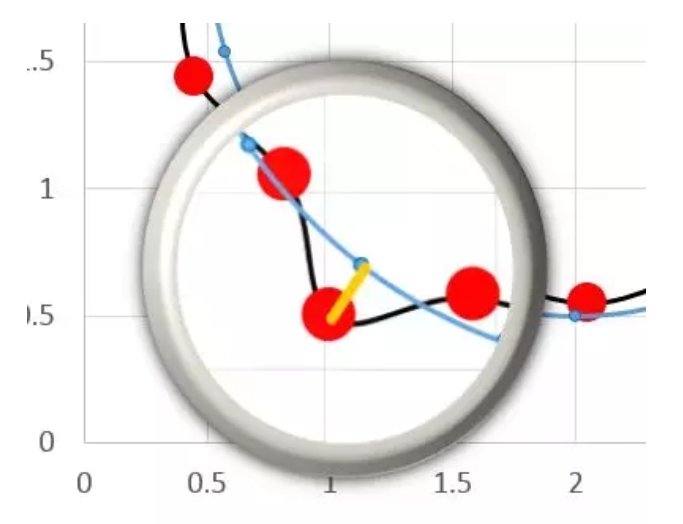
首先，我们假设有这样一个理想圆的存在，如下图：
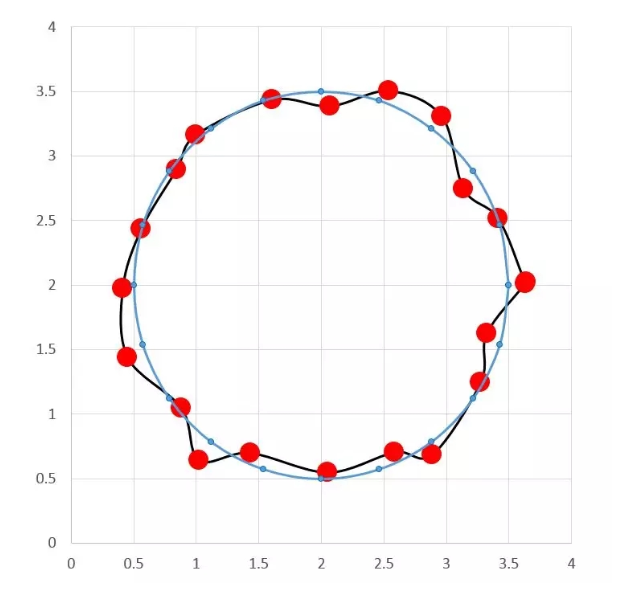
接下来我们分析一下这个理想圆存在的条件：
对比实际测量点与理想圆相应位置点（每间隔18°位置），他们之间的距离就是加工误差，用黄色线段表示：
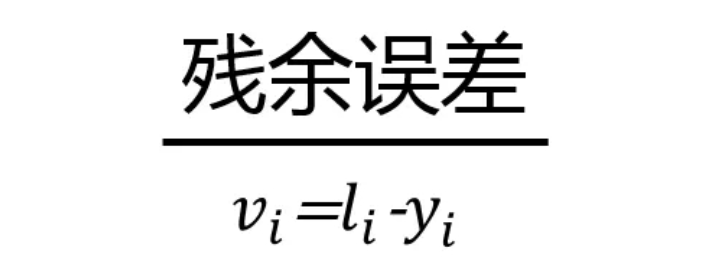
其中v表示残余误差，l表示实测点，y表示理想点。最理想的拟合圆应该能够使所有测点残余误差平方和为最小，因此应该满足如下表达式：
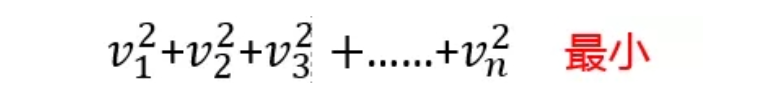
这就是最小二乘法。
“推荐阅读”
【本文标签】：
蔡司雷竞技raybet1 蔡司三次元 蔡司工业CT 蔡司显微镜 蔡司3D扫描仪 蔡司影像仪
【责任编辑】：雷竞技免费下载 测量 版权所有： //www.bengirmann.com转载请注明出处
【责任编辑】：雷竞技免费下载 测量 版权所有： //www.bengirmann.com转载请注明出处
扫描关注我们